Department of Physics and Astronomy

Physics 8140: Nuclear and Heavy-Ion Theory

Part A: Low-energy nuclear structure and reactions (Prof. Umar, Fall 2021)

Radioactive Ion Beam (RIB) physics: the frontiers of the neutron dripline and the island of superheavy elements

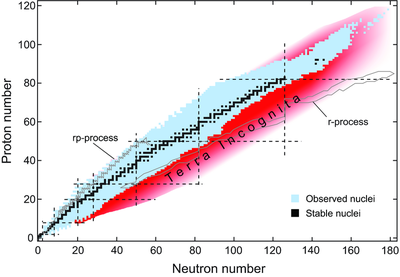
One of the fundamental questions of nuclear structure physics is: what are the limits of nuclear stability? How many neutrons can we add to a given nuclear isotope before it becomes unstable against spontaneous neutron emission (neutron radioactivity)? If one connects the isotopes with zero neutron separation energy, S_n=0, in the nuclear chart one obtains the neutron dripline. Similarly, the proton dripline is defined by the condition S_p=0. There are less than 300 stable nuclear isotopes to be found in nature (represented by small black dots in figure above). However, an additional 2700 isotopes have been created in experiments, most of these in reactions using low-energy heavy-ion accelerators. Nuclei in between the proton and neutron driplines are unstable against beta-decay. Nuclei outside the driplines decay by spontaneous neutron emission or proton radioactivity.

The neutron-rich side, in particular, exhibits thousands of nuclear isotopes still to be explored (see "terra incognita" in figure above). Some of these exotic nuclei can be studied with existing first-generation Radioactive Ion Beam Facilities. Several countries are constructing new 'second generation' RIB facilities (RIKEN in Japan, FAIR in Germany, GANIL in France). In the United States, construction has begun of FRIB (Facility for Rare Isotope Beams) at Michigan State University. Another frontier is the production of new superheavy elements in heavy-ion fusion reactions, in particular around the predicted "island of stability" with proton numbers Z=114, 120, 126 and neutron number N=184.

Theories predict profound differences between the known isotopes near stability and the exotic nuclei at the driplines: for neutron-rich nuclei, as the Fermi level approaches the particle continuum at E=0, weakly bound neutron states couple strongly to the continuum giving rise to neutron halos and neutron skins. Theories also expect large pairing correlations and new types of collective modes, a weakening of the spin-orbit force leading to a quenching of the shell gaps, and perhaps new magic numbers.

Furthermore, Radioactive Ion Beam Facilities will allow us to address fundamental questions in nuclear astrophysics: more than half of all elements heavier than iron are thought to be produced in supernovae explosions by the rapid neutron capture process (r-process). The r-process path contains many exotic neutron-rich nuclei which can only be studied with these new heavy-ion accelerators.

Class meetings and office hours

Class meetings: Tuesday and Thursday, 09:30 am, SC 6614
Office hours: Most of the time, you will find me in my office. Please feel free to drop by my office whenever you have any questions, and I will try to accomodate you if possible.

Contact Information

Instructor: Professor Sait Umar
Phone: 615-322-5035
Office: Stevenson Center, 6th floor, room 6626
e-mail: sait.a.umar@vanderbilt.edu

Phys 8140 course description (Bulletin of the Graduate School)

Basic experimental facts and phenomenological models (shell model and collective model). Nucleon-nucleon interaction, mean-field theories of nuclear structure (Hartree-Fock, BCS pairing, HFB, RPA and QRPA). Ab-initio calculations for light nuclei. Time-dependent Hartree-Fock calculations of heavy-ion reactions. Prerequisite: PHYS 8030. [3]

The aim of this course

The aim of theoretical nuclear physics is to study the quantum many-particle aspects of two of nature's four fundamental forces: the strong and the weak interaction. Depending upon the relative energy of the nuclear constituents, very different theoretical descriptions are needed:

Low-energy nuclear structure and reaction phenomena are described in terms of protons and neutrons which interact via a nucleon-nucleon potential that depends on the positions, momenta, spins and isospins of the nucleons. For relatively light nuclei, non-relativistic "ab-initio" calculations are possible, but heavier systems require a mean-field approximation. Alternatively, relativistic mean-field theories have been developed in which pointlike nucleons are described by the Dirac equation, interacting via classical meson fields.

In the medium-energy regime, particle creation and annihilation becomes a dominant feature; also, it is no longer sufficient to consider just the nucleons themselves, but other low-lying baryonic resonances and light mesons must be taken into account. The appropriate theoretical framework is the quantum theory of interacting baryon and meson fields.

At relativistic energies, the quark substructure of the baryons and mesons comes into play, and the proper starting point of the theory is the Lagrangian of Quantum Chromodynamics (QCD).

Almost all interacting quantum many-particle systems cannot be adequately described by perturbation theory, a powerful tool which governs most of elementary particle physics. In fact, the interesting physical observables (e.g. the Hartree-Fock or BCS ground state energy of the many-body quantum system) are equivalent to an infinite sum of perturbative diagrams! This requires the development of new many-body approximation schemes. Because of the mathematical complexity of the quantum many-body equations, a numerical implementation on scientific workstations and supercomputers becomes necessary.

Phys 8140 textbook and Course Website

I will not use any particular textbook. Rather, the lecture material will be drawn from a variety of textbooks and review articles (see the "Bibliography" section of this Website for details). All lecture notes and PowerPoint presentations will be posted (in PDF format) in the "Lecture materials" section of the Website.

Phys 8140 Website:     http://compsci.cas.vanderbilt.edu/~umar/p8140/

Phys-8140 prerequisites

Quantum Mechanics 8030.